Der ,Prime Climb’ Bleistift, die Schachtel und das Schaubild steigen in 6ern auf. Man fragt sich nun, welche Regelmäßigkeiten erscheinen, wenn sie in 3ern, 4ern, 5ern, 7ern, 8ern, 9ern, 10ern aufsteigen.
Verteile die Arbeit unter Deinen Freunden/ Teilnehmern einer Mathe-AG/ Deinen KlassenkameradInnen und baue ,Prime Climb’ Schachteln, die auf dem gleichseitigen Dreieck, dem Quadrat, dem regelmäßigen Fünfeck … u.s.w. basieren.
Für die 3er könnte man eine Toblerone-Packung nehmen; für die 4er eine Milchtüte; aber da Du noch die Zahlen drumherum schreiben musst, ist es besser, weißen Karton zu nehmen.
Das Numdrum selbst verläuft in 10ern, deshalb brauchen wir keine 10seitige Schachtel zu machen – es sei denn Du willst, dass alle Schachteln gleich aussehen. Sie werden auch dann alle gleich aussehen, wenn Du sie alle baust wie das Numdrum: als Zylinder, nicht als Prismen; ganz wie Du willst.
Ein Schaubild herzustellen ist schwieriger als eine Schachtel. Hier sind Tipps für beide.
Ohne besonderen Grund haben wir für unser Beispiel die 5er gewählt.
Eine ,Prime Climb’ Schachtel in 5ern aufsteigend
Die Schachtel braucht keinen Boden und keinen Deckel. Aber sie braucht eine Klebefalz, um die aufeinandertreffenden Ränder zusammenzukleben.
Trage die Zahlen auf, bevor Du die Schachtel faltest.
Wenn Du eine Küchen- oder Toilettenpapierrolle entrollst, hast Du ein sehr langes Parallelogramm vor Dir. Denk daran, wenn Du Deine Schachtel baust:
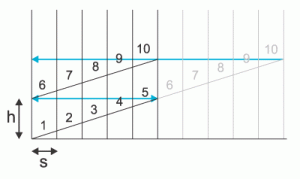
h sollte 2 x so hoch sein wie die Zahlen.
Wie Du ausrechnen kannst, muss die Gesamthöhe 100/5 x h = 20 h sein.
s sollte 3/2 x so breit sein wie eine breite 2stellige Zahl, z.B. 44.
Du kannst die Zahlen mit der Hand zeichnen oder die Zahlen als Abziehbilder auftragen oder den Computer benutzen und das Ergebnis geradewegs auf die Pappe drucken. Damit das Ganze hält, laminiere die Pappe. Du kannst dann non-permanent Filzstifte benutzen, um die Linien (genauer gesagt die 3-D Spiralen) zu ziehen, die die Vielfachen der gewählten Zahl verbinden.
Ein ,Prime Climb’ Schaubild in 5ern aufsteigend
Die Grafik ist ein Kreis mit 5 Kreisausschnitten, jeder 360°/5 = 72°.
Eine Spirale (vom Typ ,Archimedes’) windet sich aus der Mitte heraus.
Um dies mit der Hand zu zeichnen, muss man konzentrische Kreise ziehen mit gleichgroßen Zwischenräumen.
Deine Spiral beginnt im Mittelpunkt und verbindet die Schnittpunkte der aufeinanderfolgenden Kreise mit den aufeinanderfolgenden Linien:
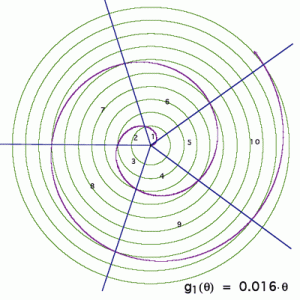
Eine einfachere Lösung ist es, eine Software für dynamische Geometrie, z.B. ,Geometer’s Sketchpad’, zu benutzen.
Wähle das ,polare’ Koordinatensystem. Für das Schaubild in aufsteigenden 6ern benutzen wir die Gleichung f(θ) = 0,0025θ, aber für die 5er muss sich Deine Spirale enger winden. Versuche f(θ) = 0,0020θ.
Wie in unserem Diagramm zu sehen, kannst Du die radialen Linien ziehen und auch die Zahlen drucken.
