
 |
A 9 x 9 multiplication square has 81 cells. But these contain only 36 different numbers. A maths teacher called Jon Millington found that these could be shared between 9 objects in such a way that, by putting them in the correct order and setting them in a row, you could make each row of the 9 x 9 multiplication square - that is to say, each of the 'times tables' up to 9 x 9.
To set up a tables race on a standard school double desk, use tetrahedra (triangular pyramids) and the spaces between 10 square-based pyramids:
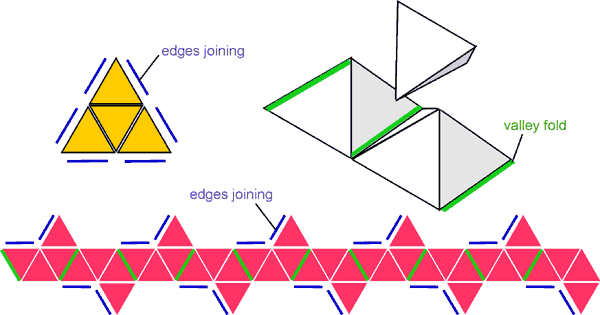
Only equilateral triangles are needed. The easiest way to make the solids is from Polydron (or other kit of interconnecting tiles). Use yellow for the tetrahedra so that the numbers show up. Use red (say) for the pyramid chain. Make 2 sets so that, instead of racing against the clock, you can race against an opponent. Sit at the long sides of the desk, facing each other across it. You each make your times table so that it faces you. In place of the spinner, make a die with 8 faces. The die is a regular octahedron, needing 8 more triangles - blue (say). Sellotape the edges so that it doesn't break up when thrown:
Altogether therefore you will need:
2 x 9 x 4 = 72 yellow triangles,
2 x 10 x 4 = 80 red triangles,
1 x 8 = 8 blue triangles.
Use dri-wipe pen for the numbers.
Here is one way to distribute the numbers between the tetrahedra:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 18 | 24 | 14 | 15 | 12 | 20 | 16 | 21 | 10 |
| 32 | 45 | 36 | 42 | 56 | 63 | 27 | 25 | 28 |
| 35 | 49 | 40 | 72 | 81 | 64 | 30 | 54 | 48 |
How can the 36 numbers be allocated to their 9 tetrahedra?
What conditions must be satisfied?
Give each tetrahedron a colour:

On the multiplication square each tetrahedron must occur exactly once in every row and column: in other words, the coloured cells must form a 'Latin' square. As a consequence, each tetrahedron is represented 9 times on the square. The 4 distinct faces account for 4 of these cells. The remaining 5 are accounted for in two ways:
1. the commutative property means that every cell is reflected in the main diagonal: 4 x 6 = 6 x 4.
2. some numbers factorise in more than one way: 4 x 6 = 3 x 8.
The number 24, then, occurs 4 times in different guises: as 4 x 6, 6 x 4, 3 x 8, 8 x 3.
And these cells lie on a hyperbola:
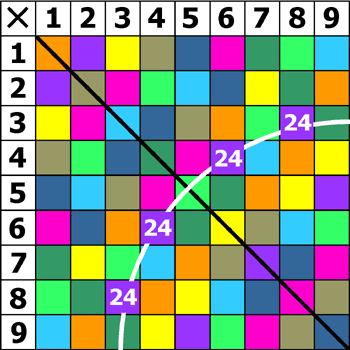
Squares lie on the main diagonal of the multiplication square, which is to
say that the commutative property reflects a square on to itself. This has an
important consequence:
each non-square occurs an even number of times;
each square occurs an odd number of times.
Because each tetrahedron is repeated 9 times - an odd number - and only squares can contribute odd numbers, there must be exactly one square on each tetrahedron.
The squares fall into 2 sets: those with just 1 entry on the multiplication square and those with 3.
For those with 1 entry, the remaining 3 faces of the tetrahedron must account for 9 - 1 = 8 entries, each of which must be an even number. The only solution in positive integers to that equation is: 8 = 2 + 2 + 4. 2 numbers must therefore occur twice but one 4 times.
For those with 3 entries, the remaining 3 faces account for 9 - 3 = 6 entries, splitting 2-2-2.
The numbers which occur 4 times are: 6, 8, 12, 18, 24. These must be paired in some order with the corresponding squares: 1, 25, 49, 64, 81. Some pairings fail: the numbers lie in the same row or column and must therefore be given different colours: 1-6, 1-8, 8-64, 24-64, 18-81. Even so, many possibilities remain open at this stage. But every pair of numbers you put on a tetrahedron must pass the 'colour' test. So, the more numbers you add to each, the harder the task becomes. This difficulty is compounded by the fact that you have fewer left to choose from.
The problem is so difficult you may decide to program a computer to find the 9 sets of numbers for you. This is what Jon Millington did.
If you want to tackle it by hand, write each number on a separate card and make a 9 x 4 grid to put them on. You can fix one number on each tetrahedron by choosing one of the 9 tables - say the 1s: 1, 2, 3, 4, 5, 6, 7, 8, 9 - or the set of squares.
Surprisingly, there is more than one solution. One has been chosen for the Tables Race. Can you find another?
Copyright © 2002 The Magic Mathworks